Minimizing Energy Cost in Electric Arc Furnace Steel Making by Optimal Control Designs
Abstract
Production cost in steel industry is a challenge issue and energy optimization is an important part. This paper proposes an optimal control design aiming at minimizing the production cost of the electric arc furnace steel making. In particular, it is shown that with the structure of an electric arc furnace, the production cost which is a linear programming problem can be solved by the tools of linear quadratic regulation control design that not only provides an optimal solution but also is in a feedback form. Modeling and control designs are validated by the actual production data sets.
1. Introduction
Steel industries recycle scrap steel using the electric arc furnace (EAF) by melting it and changing its chemical composition to produce different product grades. Obviously, steel industry is one of the greatest energy consuming sectors and there is a strong demand to decrease the use of electricity and other forms of energy in the EAF steel making.
In general, the current melting process control is manual and the production cost is not optimal. Steel industries have some nominal automation for EAFs but are mostly operator driven. Although operator intuition is invaluable for such industries, it rests on the recipes that have been effective in the past and becomes difficult to take into account all possible uncertainties unless a mathematical framework is developed for the system and an automation process is in place. It has been shown that a substantial part of the energy consumption is wasted in melting the scrap [1–3]. This illustrates that there is a tremendous opportunity for control to play.
Unlike most existing papers in the literature, this paper concerns the production cost which is related to energy consumption for melting process and the way to achieve the optimality. Therefore, the purpose of the model is different from the large part of the existing literature [1–6]. For example, in [1], an adaptive model predictive control was proposed to follow the preset trajectories. How to design the preset trajectories was not discussed. In [2], a PID controller was proposed to have the electrodes maintain constant power consumption. In [3], a model was developed but there was no discussion on how to control it. In [6], a model was proposed to achieving the maximum power input to the melting process. In all these works, minimizing control consumption was not a concern. In the work reported here, a mathematical model of EAFs is developed and its unknown parameters are then estimated. The goal of the model is to design a control algorithm that minimizes the energy consumption. The model adopted in this paper is a linear time invariant system which seems to work satisfactorily. More importantly, in the second step, optimal control inputs are calculated aiming at minimizing the production cost. Because the actual production cost is linear in the consumptions of energy and graphite electrode, the optimization is a linear programming problem. A problem of the linear programming is that it provides an open loop input design. Though optimal in the absence of model uncertainty and measurement noise, its performance in reality cannot be guaranteed under inevitable model uncertainty and measurement noise. The contribution of the paper is to show that with the particular structure of the EAF, the linear programming problem can in fact be solved by the well-known linear quadratic regulation (LQR) problem which is in a feedback form and thus is more robust than an open loop solution.
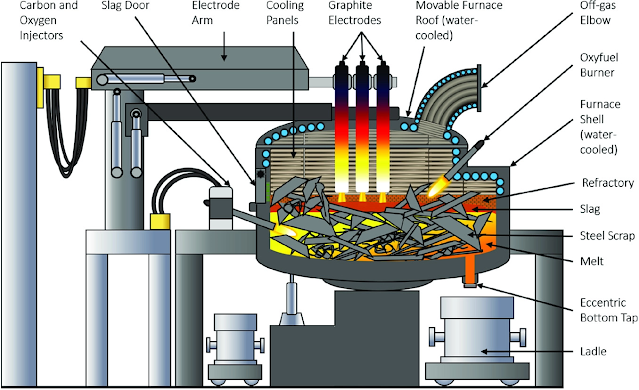
All the data sets used in this study for modeling and control validation are actual production data collected from the Gerdau Ameristeel mill facility in Wilton Iowa that is composed of a scrap shredding facility, an electric arc furnace (EAF) as shown in Figure 1, several continuous billet casters, and a rolling mill. Because of proprietary properties, no actual data value is revealed in the paper, but the modeling results and final performance improvements are shown.2. Problem Statement
In this section, we describe the system model and the goal of optimal control. Clearly, EAF models could be different for different purposes. Our goal is to optimize the production cost while the quality and efficiency are maintained. To this end, we focus on 7 key variables that provide a fairly reasonable description of the dynamics of an EAF:(i)kilowatt-hour consumption (KWH),(ii)electrode consumption (𝐼2ℎ),(iii)percentage of scrap melted (PM),(iv)average arc current (𝐼avg),(v)oxygen input (O2),(vi)gas input (Gas),(vii)carbon input (Car).
All 7 variables are either measurable or computable in real time. Among these variables, the kilowatt-hour consumption (KWH) is the consumption of electrical energy that constitutes a substantial part of the total cost, the electrode consumption (𝐼2ℎ) is the consumption of the graphite electrode that also contributes to the cost significantly, and the percentage of scrape melted (PM)) is the percentage of scrap melted which is a quality constraint on the melting control. At the end of each melting process, has to be 100(%). Other 4 variables are electrical energy input and chemical energy inputs (oxygen), (gas), and (carbon), respectively. All 4 energy inputs contribute to the total cost and among them is the most expensive one.
Based on the physics, the increments of the kilowatt-hour consumption (KWH) and the electrode consumption (𝐼2ℎ) from time 𝑘𝛿𝑡 to (𝑘 + 1)𝛿𝑡 are directly related to the current 𝐼avg in the interval [𝑘𝛿𝑡,(𝑘+1)𝛿𝑡). On the other hand, the percentage of scrape melted (PM) is related to all energy inputs during the same period including the electrical energy as well as chemical energy. The EAF assumes the following structure:
6. Conclusion and Future Work
The method proposed for the optimal control strategy of an arc furnace provides a closed loop robust scheme that optimizes the production cost of the EAF steel making. In this study, we focus on 7 key variables and a linear modeling. In the future, other minor variables and possibly nonlinear effects could and should be considered. It is expected that by combining all the factors, the production cost can be reduced further. Also, the strategy developed in this paper can be extended to other applications in which the cost function is linear and the control design used is quadratic.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Acknowledgment
This work was supported in part by the Iowa Energy Center Grant 09-01.
References
- R. Balan, V. Maties, O. Hancu, S. Stan, and L. Ciprian, “Modeling and control of an electric arc furnace,” in Proceedings of the 15 Mediterranean Conference on Control and Automation, pp. 1–6, Athens, Greece, July 2007.
- B. Boulet, G. Lalli, and M. Ajersch, “Modeling and control of an electric arc furnace,” in Proceedings of the American Control Conference, pp. 3060–3064, Denver, Colo, USA, June 2003.
- Ü. Çamdali and M. Tunç, “Modelling of electric energy consumption in the AC electric arc furnace,” International Journal of Energy Research, vol. 26, no. 10, pp. 935–947, 2002.
- Anuradha, K. B. Muni, and A. Kumar, “Modeling of EFA and control algorithms for voltage flicker mitigation using DSTATCOM,” in Proceedings of the 16th National Power Systems Conference, Hyderabad, India, December 2010.
- M. Han and X. Huang, “Greedy kernel components acting on ANFIS to predict BOF steelmaking endpoint,” in Proceedings of the 17th World Congress, International Federation of Automatic Control (IFAC '08), Seoul, South Korea, July 2008.
- L. Hocine, D. Yacine, K. M. Samira, and B. Kamel, “Closely parametrical model for an electrical arc furnace,” World Academy of Science, Engineering and Technology, vol. 40, pp. 96–100, 2008.
- F. Lewis and V. Syrmos, Optimal Control, John Wiley & Sons, New York, NY, USA, 1995.
- K. Zhou, J. Doyle, and K. Glover, Robust and Optimal Control, Prentice Hall, Upper Saddle River, NJ, USA, 1995.
Copyright
Copyright © 2014 Er-Wei Bai. This is an open-access article distributed under the
Creative Commons Attribution License, which permits unrestricted use, distribution,
and reproduction in any medium, provided the original work is properly cited.

.jpg)








没有评论:
发表评论